数据分析与多项式计算思维导图
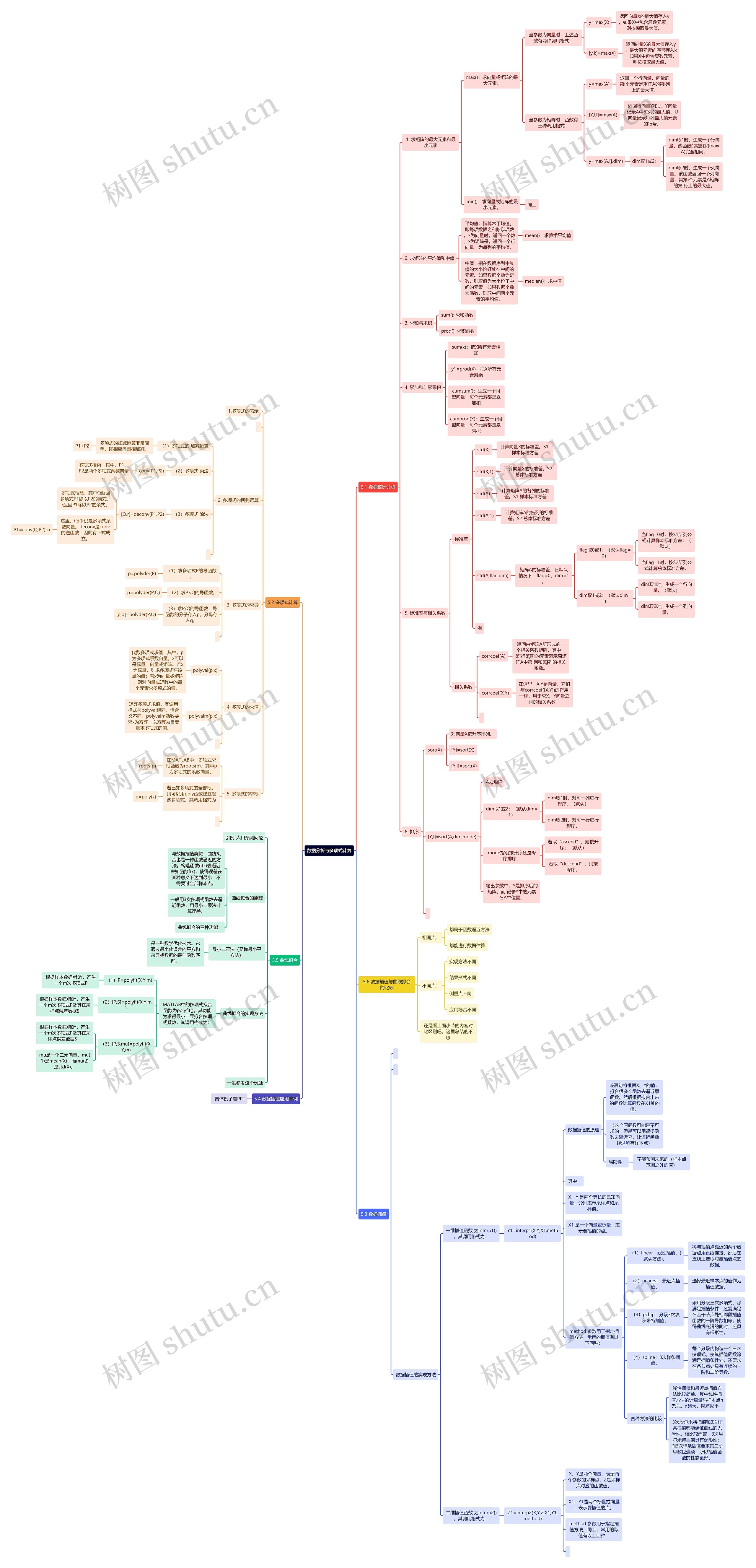
MATLAB基础知识——数据分析与多项式计算
树图思维导图提供 数据分析与多项式计算 在线思维导图免费制作,点击“编辑”按钮,可对 数据分析与多项式计算 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:93dba05ded8571bdc740235cb9d32f97
思维导图大纲
数据分析与多项式计算思维导图模板大纲
5.1 数据统计分析
1. 求矩阵的最大元素和最小元素
max():求向量或矩阵的最大元素。
当参数为向量时,上述函数有两种调用格式:
y=max(X)
返回向量X的最大值存入y,如果X中包含复数元素,则按模取最大值。
[y,k]=max(X)
返回向量X的最大值存入y,最大值元素的序号存入k,如果X中包含复数元素,则按模取最大值。
当参数为矩阵时,函数有三种调用格式:
y=max(A)
返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值。
[Y,U]=max(A)
返回行向量Y和U,Y向量记录A中每列的最大值,U向量记录每列最大值元素的行号。
y=max(A,[],dim)
dim取1或2:
dim取1时,生成一个行向量。该函数的功能和max(A)完全相同;
dim取2时,生成一个列向量。该函数返回一个列向量,其第i个元素是A矩阵的第i行上的最大值。
min():求向量或矩阵的最小元素。
同上
2. 求矩阵的平均值和中值
平均值:指算术平均值,即每项数据之和除以项数。x为向量时,返回一个数;x为矩阵是,返回一个行向量,为每列的平均值。
mean():求算术平均值
中值:指在数据序列中其值的大小恰好处在中间的元素。如果数据个数为奇数,则取值为大小位于中间的元素;如果数据个数为偶数,则取中间两个元素的平均值。
median():求中值
3. 求和与求积
sum(): 求和函数
prod(): 求积函数
4. 累加和与累乘积
sum(x):把X所有元素相加
y1=prod(X):把X所有元素累乘
cumsum():生成一个同型向量,每个元素都是累加和
cumprod(X):生成一个同型向量,每个元素都是累乘积
5. 标准差与相关系数
标准差
std(X)
计算向量X的标准差。S1 样本标准方差
std(X,1)
计算向量X的标准差。S2 总体标准方差
std(A)
计算矩阵A的各列的标准差。S1 样本标准方差
std(A,1)
计算矩阵A的各列的标准差。S2 总体标准方差
std(A,flag,dim)
矩阵A的标准差,在默认情况下,flag=0,dim=1。
flag取0或1:(默认flag=0)
当flag=0时,按S1所列公式计算样本标准方差;(默认)
当flag=1时,按S2所列公式计算总体标准方差。
dim取1或2:(默认dim=1)
dim取1时,生成一个行向量。(默认)
dim取2时,生成一个列向量。
例
相关系数
corrcoef(A)
返回由矩阵A所形成的一个相关系数矩阵,其中,第i行第j列的元素表示原矩阵A中第i列和第j列的相关系数。
corrcoef(X,Y)
在这里,X,Y是向量,它们与corrcoef([X,Y])的作用一样,用于求X、Y向量之间的相关系数。
6. 排序
sort(X)
对向量X按升序排列。
[Y]=sort(X)
[Y,I]=sort(X)
[Y,I]=sort(A,dim,mode)
A为矩阵
dim取1或2:(默认dim=1)
dim取1时,对每一列进行排序。(默认)
dim取2时,对每一行进行排序。
mode指明按升序还是降序排序,
若取“ascend”,则按升序;(默认)
若取“descend”,则按降序,
输出参数中,Y是排序后的矩阵,而I记录Y中的元素在A中位置。
5.2 多项式计算
1.多项式的表示
2. 多项式的四则运算
(1)多项式的 加减运算
多项式的加减运算非常简单,即相应向量相加减。
P1+P2
(2)多项式 乘法
conv(P1,P2)
多项式相乘,其中,P1、P2是两个多项式系数向量。
(3)多项式 除法
[Q,r]=deconv(P1,P2)
多项式相除,其中Q返回多项式P1除以P2的商式,r返回P1除以P2的余式。
这里,Q和r仍是多项式系数向量。deconv是conv的逆函数,因此有下式成立。
P1=conv(Q,P2)+r
3. 多项式的求导
(1)求多项式P的导函数。
p=polyder(P)
(2)求P×Q的导函数。
p=polyder(P,Q)
(3)求P/Q的导函数,导函数的分子存入p,分母存入q。
[p,q]=polyder(P,Q)
4. 多项式的求值
polyval(p,x)
代数多项式求值,其中,p为多项式系数向量,x可以是标量、向量或矩阵。若x为标量,则求多项式在该点的值;若x为向量或矩阵,则对向量或矩阵中的每个元素求多项式的值。
polyvalm(p,x)
矩阵多项式求值,其调用格式与polyval相同,但含义不同。polyvalm函数要求x为方阵,以方阵为自变量求多项式的值。
5. 多项式的求根
在MATLAB中,多项式求根函数为roots(p),其中p为多项式的系数向量。
roots(p)
若已知多项式的全部根,则可以用poly函数建立起该多项式,其调用格式为:
p=poly(x)
5.6 数据插值与曲线拟合的比较
相同点:
都属于函数逼近方法
都能进行数据估算
不同点:
实现方法不同
结果形式不同
侧重点不同
应用场合不同
还是看上面小节的内容对比区别吧,这里总结的不够
5.5 曲线拟合
引例-人口预测问题
曲线拟合的原理
与数据插值类似,曲线拟合也是一种函数逼近的方法。构造函数g(x)去逼近未知函数f(x),使得误差在某种意义下达到最小,不需要过全部样本点。
一般用3次多项式函数去逼近函数,用最小二乘法计算误差。
曲线拟合的三种功能:
最小二乘法(又称最小平方法)
是一种数学优化技术。它通过最小化误差的平方和来寻找数据的最佳函数匹配。
曲线拟合的实现方法
MATLAB中的多项式拟合函数为polyfit(),其功能为求得最小二乘拟合多项式系数,其调用格式为:
(1)P=polyfit(X,Y,m)
根据样本数据X和Y,产生一个m次多项式P
(2)[P,S]=polyfit(X,Y,m)
根据样本数据X和Y,产生一个m次多项式P及其在采样点误差数据S
(3)[P,S,mu]=polyfit(X,Y,m)
根据样本数据X和Y,产生一个m次多项式P及其在采样点误差数据S,
mu是一个二元向量,mu(1)是mean(X),而mu(2)是std(X)。
一般参考这个例题
5.3 数据插值
数据插值的实现方法
一维插值函数 为interp1(),其调用格式为:
Y1=interp1(X,Y,X1,method)
数据插值的原理
该语句将根据X、Y的值,拟合很多个函数去逼近原函数。然后根据拟合出来的函数计算函数在X1处的值。
(这个原函数可能是不可求的,但是可以用很多函数去逼近它,让逼近函数经过所有样本点)
局限性:
不能预测未来的(样本点范围之外的值)
其中,
X、Y 是两个等长的已知向量,分别表示采样点和采样值。
X1 是一个向量或标量,表示要插值的点。
method 参数用于指定插值方法,常用的取值有以下四种:
(1)linear:线性插值,(默认方法)。
将与插值点靠近的两个数据点用直线连接,然后在直线上选取对应插值点的数据。
(2)nearest:最近点插值。
选择最近样本点的值作为插值数据。
(3)pchip:分段3次埃尔米特插值。
采用分段三次多项式,除满足插值条件,还需满足在若干节点处相邻段插值函数的一阶导数相等,使得曲线光滑的同时,还具有保形性。
(4)spline:3次样条插值。
每个分段内构造一个三次多项式,使其插值函数除满足插值条件外,还要求在各节点处具有连续的一阶和二阶导数。
四种方法的比较
线性插值和最近点插值方法比较简单。其中线性插值方法的计算量与样本点n无关。n越大,误差越小。
3次埃尔米特插值和3次样条插值都能保证曲线的光滑性。相比较而言,3次埃尔米特插值具有保形性;而3次样条插值要求其二阶导数也连续,所以插值函数的性态更好。
二维插值函数 为interp2(),其调用格式为:
Z1=interp2(X,Y,Z,X1,Y1,method)
X、Y是两个向量,表示两个参数的采样点,Z是采样点对应的函数值。
X1、Y1是两个标量或向量,表示要插值的点。
method 参数用于指定插值方法,同上,常用的取值有以上四种:
5.4 数据插值应用举例
具体例子看PPT
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 9.战斗的基督教 在线思维导图免费制作,点击“编辑”按钮,可对 9.战斗的基督教 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:33d168acd0cd9f767f809c7a5df86e3a










 上海工商
上海工商