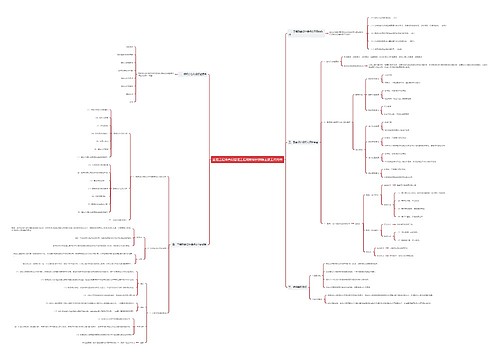
证券投资管理常用描述性统计概念思维导图
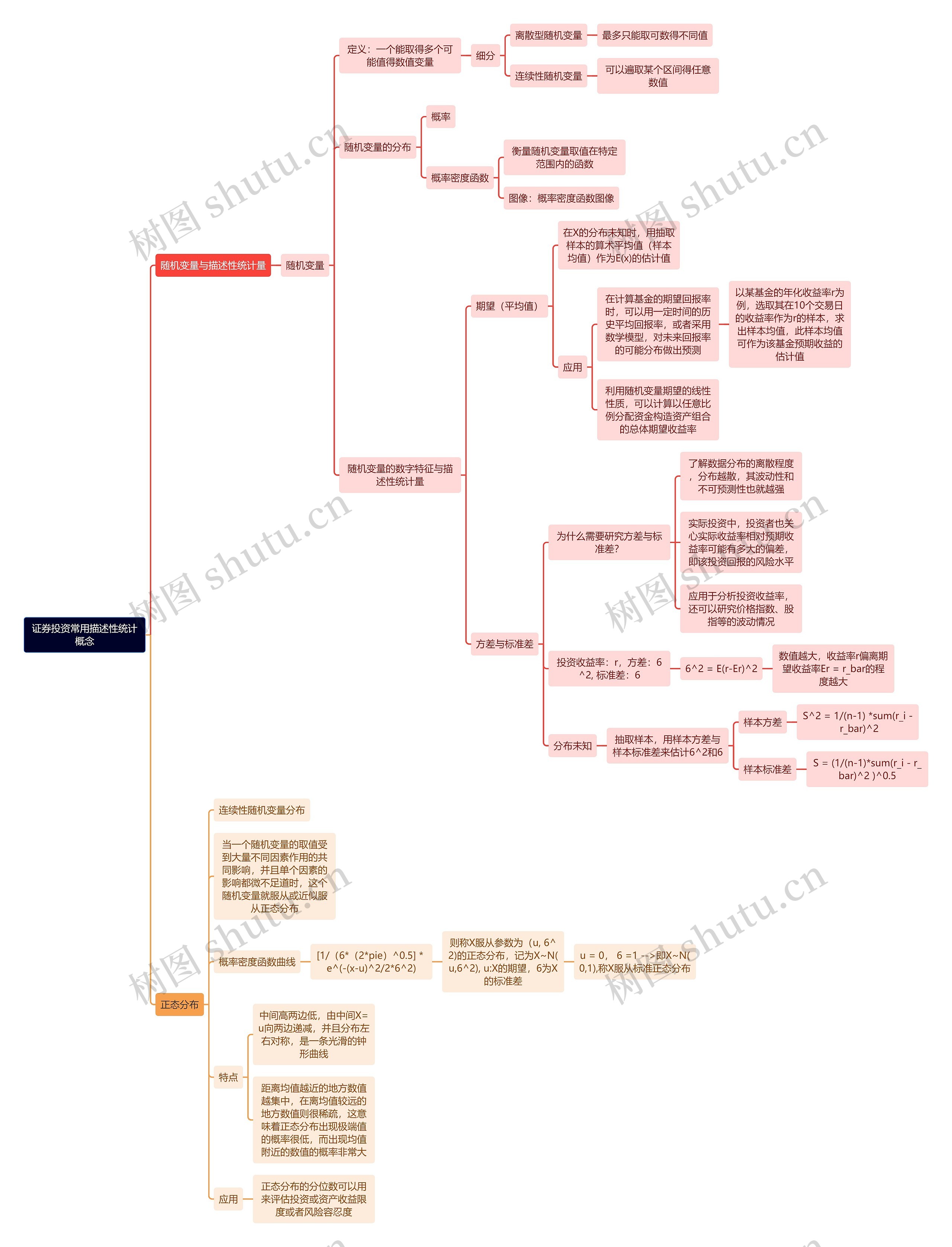
证券投资管理随机变量与描述性统计量
树图思维导图提供 证券投资管理常用描述性统计概念 在线思维导图免费制作,点击“编辑”按钮,可对 证券投资管理常用描述性统计概念 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ebcc74bf350fa974f5138d95e970683c
思维导图大纲
证券投资常用描述性统计概念思维导图模板大纲
随机变量与描述性统计量
随机变量
定义:一个能取得多个可能值得数值变量
细分
离散型随机变量
最多只能取可数得不同值
连续性随机变量
可以遍取某个区间得任意数值
随机变量的分布
概率
概率密度函数
衡量随机变量取值在特定范围内的函数
图像:概率密度函数图像
随机变量的数字特征与描述性统计量
期望(平均值)
在X的分布未知时,用抽取样本的算术平均值(样本均值)作为E(x)的估计值
应用
在计算基金的期望回报率时,可以用一定时间的历史平均回报率,或者采用数学模型,对未来回报率的可能分布做出预测
以某基金的年化收益率r为例,选取其在10个交易日的收益率作为r的样本,求出样本均值,此样本均值可作为该基金预期收益的估计值
利用随机变量期望的线性性质,可以计算以任意比例分配资金构造资产组合的总体期望收益率
方差与标准差
为什么需要研究方差与标准差?
了解数据分布的离散程度,分布越散,其波动性和不可预测性也就越强
实际投资中,投资者也关心实际收益率相对预期收益率可能有多大的偏差,即该投资回报的风险水平
应用于分析投资收益率,还可以研究价格指数、股指等的波动情况
投资收益率:r,方差:6^2, 标准差:6
6^2 = E(r-Er)^2
数值越大,收益率r偏离期望收益率Er = r_bar的程度越大
分布未知
抽取样本,用样本方差与样本标准差来估计6^2和6
样本方差
S^2 = 1/(n-1) *sum(r_i - r_bar)^2
样本标准差
S = (1/(n-1)*sum(r_i - r_bar)^2 )^0.5
正态分布
连续性随机变量分布
当一个随机变量的取值受到大量不同因素作用的共同影响,并且单个因素的影响都微不足道时,这个随机变量就服从或近似服从正态分布
概率密度函数曲线
[1/(6*(2*pie)^0.5] * e^(-(x-u)^2/2*6^2)
则称X服从参数为(u, 6^2)的正态分布,记为X~N(u,6^2), u:X的期望,6为X的标准差
u = 0, 6 =1 -->即X~N(0,1),称X服从标准正态分布
特点
中间高两边低,由中间X=u向两边递减,并且分布左右对称,是一条光滑的钟形曲线
距离均值越近的地方数值越集中,在离均值较远的地方数值则很稀疏,这意味着正态分布出现极端值的概率很低,而出现均值附近的数值的概率非常大
应用
正态分布的分位数可以用来评估投资或资产收益限度或者风险容忍度
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 1113爆卡会总结会会议纪要 在线思维导图免费制作,点击“编辑”按钮,可对 1113爆卡会总结会会议纪要 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:aaf6c152a765d5821e8e1787f2b3226e





 上海工商
上海工商