高中数学必修五数列知识点思维导图
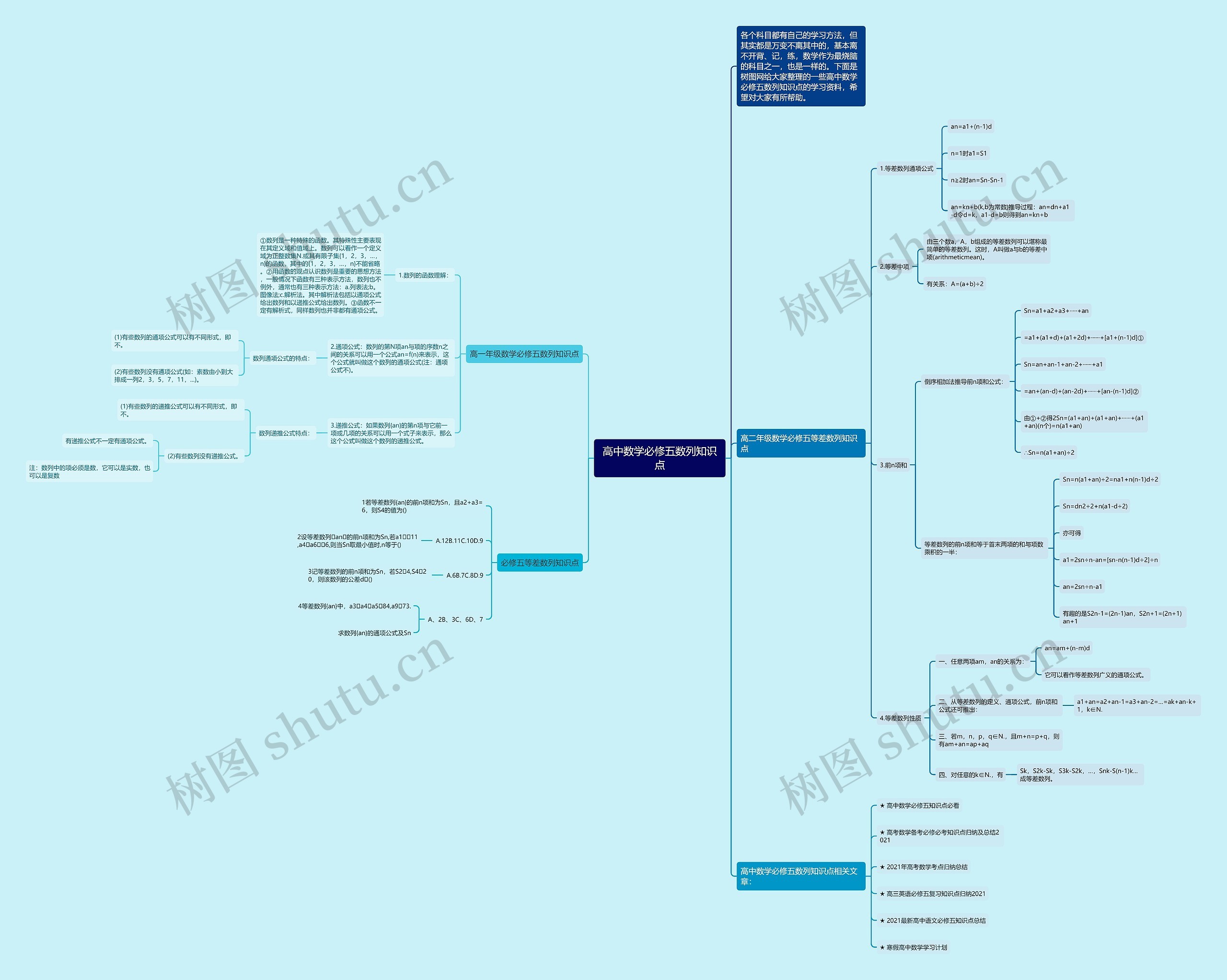
高中数学必修五数列知识点思维导图,包含以下内容:1.数列的函数理解:数列是一种特殊的函数,在数学中具有重要的意义,其通常有三种表示方法,包含列表法、图像法和解析法。
2.通项公式:数列的第N项an与项的序数n之间的关系可以用一个公式an=f(n)来表示,这个公式就叫做这个数列的通项公式。但有些数列没有通项公式,不能通过公式计算。
3.递推公式:如果数列的第n项与他前一项或几项的关系可以用一个式子来表示,那么这个公式叫做这个数列的递推公式。有些数列的递推公式可以有不同形式,但有些数列没有递推公式。
4.等差数列知识点:等差数列通常有等差数列通项公式、等差中项和前n项和。其中等差数列的前n项和等于首末两项的和与项数乘积的一半。
学习这些数列知识点,不仅要记背公式,更要理解每个概念的内涵和适用条件,这样才能灵活运用到实际问题中。
思维导图大纲
高中数学必修五数列知识点思维导图模板大纲
各个科目都有自己的学习方法,但其实都是万变不离其中的,基本离不开背、记,练,数学作为最烧脑的科目之一,也是一样的。下面是树图网给大家整理的一些高中数学必修五数列知识点的学习资料,希望对大家有所帮助。
高一年级数学必修五数列知识点
1.数列的函数理解:
①数列是一种特殊的函数。其特殊性主要表现在其定义域和值域上。数列可以看作一个定义域为正整数集N.或其有限子集{1,2,3,…,n}的函数,其中的{1,2,3,…,n}不能省略。②用函数的观点认识数列是重要的思想方法,一般情况下函数有三种表示方法,数列也不例外,通常也有三种表示方法:a.列表法;b。图像法;c.解析法。其中解析法包括以通项公式给出数列和以递推公式给出数列。③函数不一定有解析式,同样数列也并非都有通项公式。
2.通项公式:数列的第N项an与项的序数n之间的关系可以用一个公式an=f(n)来表示,这个公式就叫做这个数列的通项公式(注:通项公式不)。
数列通项公式的特点:
(1)有些数列的通项公式可以有不同形式,即不。
(2)有些数列没有通项公式(如:素数由小到大排成一列2,3,5,7,11,...)。
3.递推公式:如果数列{an}的第n项与它前一项或几项的关系可以用一个式子来表示,那么这个公式叫做这个数列的递推公式。
数列递推公式特点:
(1)有些数列的递推公式可以有不同形式,即不。
(2)有些数列没有递推公式。
有递推公式不一定有通项公式。
注:数列中的项必须是数,它可以是实数,也可以是复数
高二年级数学必修五等差数列知识点
1.等差数列通项公式
an=a1+(n-1)d
n=1时a1=S1
n≥2时an=Sn-Sn-1
an=kn+b(k,b为常数)推导过程:an=dn+a1-d令d=k,a1-d=b则得到an=kn+b
2.等差中项
由三个数a,A,b组成的等差数列可以堪称最简单的等差数列。这时,A叫做a与b的等差中项(arithmeticmean)。
有关系:A=(a+b)÷2
3.前n项和
倒序相加法推导前n项和公式:
Sn=a1+a2+a3+·····+an
=a1+(a1+d)+(a1+2d)+······+[a1+(n-1)d]①
Sn=an+an-1+an-2+······+a1
=an+(an-d)+(an-2d)+······+[an-(n-1)d]②
由①+②得2Sn=(a1+an)+(a1+an)+······+(a1+an)(n个)=n(a1+an)
∴Sn=n(a1+an)÷2
等差数列的前n项和等于首末两项的和与项数乘积的一半:
Sn=n(a1+an)÷2=na1+n(n-1)d÷2
Sn=dn2÷2+n(a1-d÷2)
亦可得
a1=2sn÷n-an=[sn-n(n-1)d÷2]÷n
an=2sn÷n-a1
有趣的是S2n-1=(2n-1)an,S2n+1=(2n+1)an+1
4.等差数列性质
一、任意两项am,an的关系为:
an=am+(n-m)d
它可以看作等差数列广义的通项公式。
二、从等差数列的定义、通项公式,前n项和公式还可推出:
a1+an=a2+an-1=a3+an-2=…=ak+an-k+1,k∈N.
三、若m,n,p,q∈N.,且m+n=p+q,则有am+an=ap+aq
四、对任意的k∈N.,有
Sk,S2k-Sk,S3k-S2k,…,Snk-S(n-1)k…成等差数列。
必修五等差数列知识点
1若等差数列{an}的前n项和为Sn,且a2+a3=6,则S4的值为()
A.12B.11C.10D.9
2设等差数列an的前n项和为Sn,若a111,a4a66,则当Sn取最小值时,n等于()
A.6B.7C.8D.9
3记等差数列的前n项和为Sn,若S24,S420,则该数列的公差d()
A、2B、3C、6D、7
4等差数列{an}中,a3a4a584,a973.
求数列{an}的通项公式及Sn
高中数学必修五数列知识点相关文章:
★ 高中数学必修五知识点必看
★ 高考数学备考必修必考知识点归纳及总结2021
★ 2021年高考数学考点归纳总结
★ 高三英语必修五复习知识点归纳2021
★ 2021最新高中语文必修五知识点总结
★ 寒假高中数学学习计划
相关思维导图模板


树图思维导图提供 抓住重点 在线思维导图免费制作,点击“编辑”按钮,可对 抓住重点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826

树图思维导图提供 数智技术在工程设备管理中的应用 在线思维导图免费制作,点击“编辑”按钮,可对 数智技术在工程设备管理中的应用 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f9a2de84ad9a9ceebc96385d71be9ebe








 上海工商
上海工商