位似人教版数学九年级下册教案思维导图
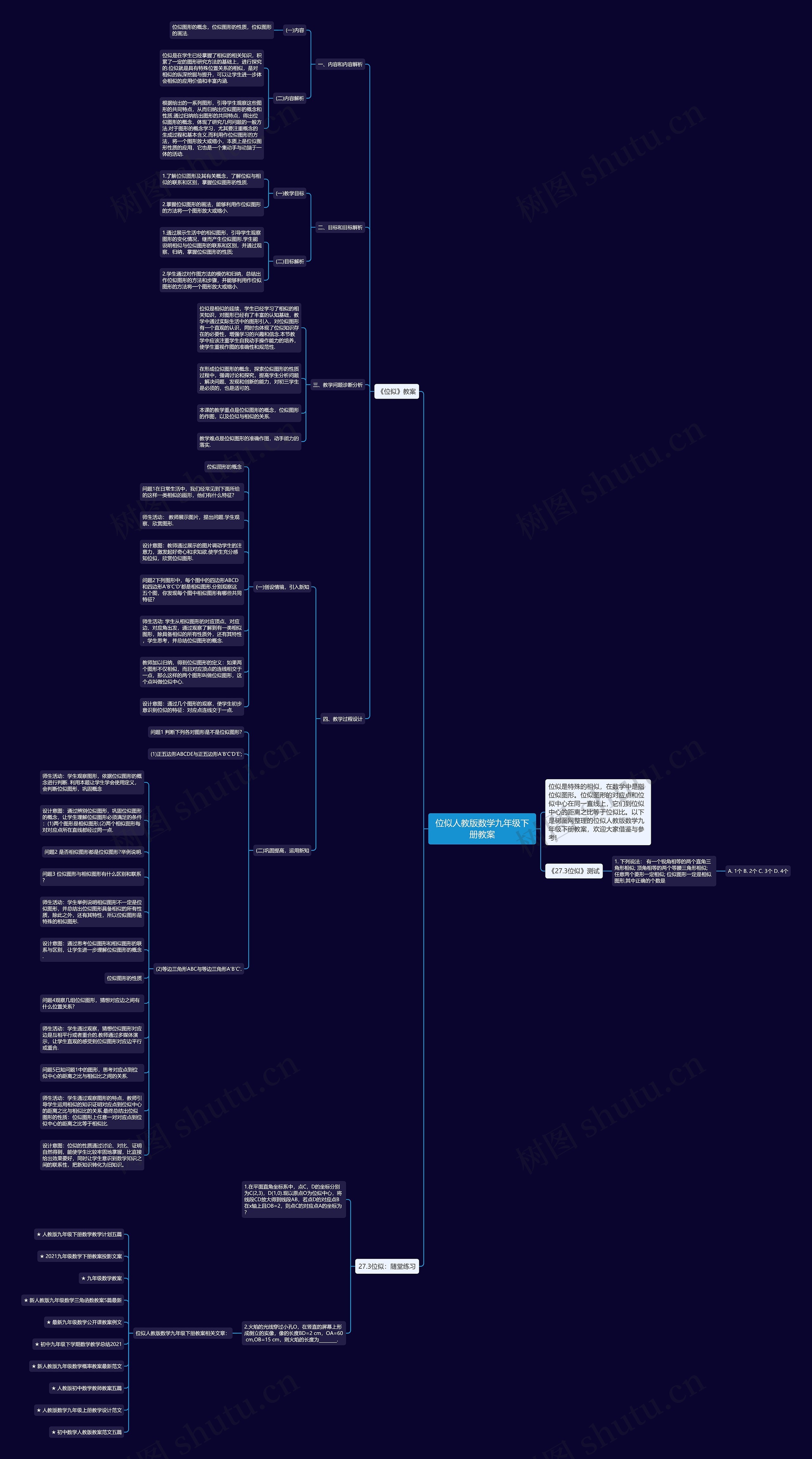
这个模板首句完整包含关键词“位似人教版数学九年级下册教案思维导图”,知识点有三个:位似图形的概念、位似图形的性质和位似与相似的联系和区别。教学目标是让学生了解位似图形有关概念,掌握作位似图形的方法,同时提高学生分析问题、解决问题、发现和创新的能力,在教学过程中,需要让学生观察、欣赏、总结位似图形的特点,引导学生猜想、证明位似图形的性质,通过这样的教学方法,使学生比较牢固地掌握知识,同时意识到数学知识之间的联系性。
思维导图大纲
位似人教版数学九年级下册教案思维导图模板大纲
位似是特殊的相似,在数学中是指位似图形。位似图形的对应点和位似中心在同一直线上,它们到位似中心的距离之比等于位似比。以下是树图网整理的位似人教版数学九年级下册教案,欢迎大家借鉴与参考!
《位似》教案
一、内容和内容解析
(一)内容
位似图形的概念,位似图形的性质,位似图形的画法.
(二)内容解析
位似是在学生已经掌握了相似的相关知识,积累了一定的图形研究方法的基础上,进行探究的.位似就是具有特殊位置关系的相似,是对相似的纵深挖掘与提升,可以让学生进一步体会相似的应用价值和丰富内涵.
根据给出的一系列图形,引导学生观察这些图形的共同特点,从而归纳出位似图形的概念和性质.通过归纳给出图形的共同特点,得出位似图形的概念,体现了研究几何问题的一般方法.对于图形的概念学习,尤其要注重概念的生成过程和基本含义.而利用作位似图形的方法,将一个图形放大或缩小,本质上是位似图形性质的应用,它也是一个集动手与动脑于一体的活动.
二、目标和目标解析
(一)教学目标
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
(二)目标解析
1.通过展示生活中的相似图形,引导学生观察图形的变化情况,继而产生位似图形.学生能说明相似与位似图形的联系和区别,并通过观察、归纳,掌握位似图形的性质;
2.学生通过对作图方法的模仿和归纳,总结出作位似图形的方法和步骤,并能够利用作位似图形的方法将一个图形放大或缩小.
三、教学问题诊断分析
位似是相似的延续,学生已经学习了相似的相关知识,对图形已经有了丰富的认知基础,教学中通过实际生活中的图形引入,对位似图形有一个直观的认识,同时也体现了位似知识存在的必要性,增强学习的兴趣和信念.本节教学中应该注重学生自我动手操作能力的培养,使学生重视作图的准确性和规范性.
在形成位似图形的概念,探索位似图形的性质过程中,强调讨论和探究,提高学生分析问题、解决问题、发现和创新的能力,对初三学生是必须的,也是适可的.
本课的教学重点是位似图形的概念,位似图形的作图,以及位似与相似的关系.
教学难点是位似图形的准确作图,动手能力的落实.
四、教学过程设计
(一)创设情境,引入新知
位似图形的概念
问题1在日常生活中,我们经常见到下面所给的这样一类相似的图形,他们有什么特征?
师生活动: 教师展示图片,提出问题.学生观察、欣赏图形.
设计意图:教师通过展示的图片调动学生的注意力,激发起好奇心和求知欲.使学生充分感知位似,欣赏位似图形.
问题2下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中相似图形有哪些共同特征?
师生活动: 学生从相似图形的对应顶点、对应边、对应角出发,通过观察了解到有一类相似图形,除具备相似的所有性质外,还有其特性,学生思考,并总结位似图形的概念.
教师加以归纳,得到位似图形的定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
设计意图:通过几个图形的观察,使学生初步意识到位似的特征:对应点连线交于一点.
(二)巩固提高,运用新知
问题1 判断下列各对图形是不是位似图形?
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
(2)等边三角形ABC与等边三角形A′B′C′.
师生活动:学生观察图形,依据位似图形的概念进行判断. 利用本题让学生学会使用定义,会判断位似图形,巩固概念
设计意图:通过辨别位似图形,巩固位似图形的概念,让学生理解位似图形必须满足的条件:(1)两个图形是相似图形;(2)两个相似图形每对对应点所在直线都经过同一点.
问题2 是否相似图形都是位似图形?举例说明.
问题3 位似图形与相似图形有什么区别和联系?
师生活动:学生举例说明相似图形不一定是位似图形,并总结出位似图形具备相似的所有性质,除此之外,还有其特性,所以位似图形是特殊的相似图形.
设计意图:通过思考位似图形和相似图形的联系与区别,让学生进一步理解位似图形的概念.
位似图形的性质
问题4观察几组位似图形,猜想对应边之间有什么位置关系?
师生活动:学生通过观察,猜想位似图形对应边是互相平行或者重合的.教师通过多媒体演示,让学生直观的感受到位似图形对应边平行或重合.
问题5已知问题1中的图形,思考对应点到位似中心的距离之比与相似比之间的关系.
师生活动:学生通过观察图形的特点,教师引导学生运用相似的知识证明对应点到位似中心的距离之比与相似比的关系.最终总结出位似图形的性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
设计意图:位似的性质通过讨论、对比、证明自然得到,能使学生比较牢固地掌握,比直接给出效果要好,同时让学生意识到数学知识之间的联系性,把新知识转化为旧知识。
《27.3位似》测试
1. 下列说法: 有一个锐角相等的两个直角三角形相似; 顶角相等的两个等腰三角形相似; 任意两个菱形一定相似; 位似图形一定是相似图形;其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
27.3位似:随堂练习
1.在平面直角坐标系中,点C,D的坐标分别为C(2,3),D(1,0).现以原点O为位似中心,将线段CD放大得到线段AB,若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为?
2.火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则火焰的长度为________.
位似人教版数学九年级下册教案相关文章:
★ 人教版九年级下册数学教学计划五篇
★ 2021九年级数学下册教案投影文案
★ 九年级数学教案
★ 新人教版九年级数学三角函数教案5篇最新
★ 最新九年级数学公开课教案例文
★ 初中九年级下学期数学教学总结2021
★ 新人教版九年级数学概率教案最新范文
★ 人教版初中数学教师教案五篇
★ 人教版数学九年级上册教学设计范文
★ 初中数学人教版教案范文五篇
相关思维导图模板


树图思维导图提供 九年级数学教案人教版文案 在线思维导图免费制作,点击“编辑”按钮,可对 九年级数学教案人教版文案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:51ecf42dc0c1e822468fa51030095157

树图思维导图提供 九年级数学下册教案投影文案 在线思维导图免费制作,点击“编辑”按钮,可对 九年级数学下册教案投影文案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:170e4267067ca1f1ab5572e578d164f8


















 上海工商
上海工商