固体自由电子理论思维导图
大学物理中有关固体自由电子理论的思维导图，包括金属自由电子气模型(CFEM)、量子力学修正的自由电子模型(QMFEM)
树图思维导图提供 固体自由电子理论思维导图 在线思维导图免费制作，点击“编辑”按钮，可对 固体自由电子理论思维导图 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：abf47afbd9a03e3397d5f5dd113158ad
思维导图大纲
固体自由电子理论思维导图思维导图模板大纲
金属自由电子气模型(CFEM)
1900年，Drude提出经典理论框架下的金属自由电子气模型(CFEM)
最外层的价电子作为自由电子参与导电
自由电子之间以及自由电子与离子之间不存在相互作用
就是说自由电子相当于理想气体，服从麦克斯韦玻尔兹曼统计
而在外加电场下，自由电子会获得一个漂移速度从而产生电流
既然服从麦克斯韦玻尔兹曼分布，在无外加电场下
进而根据这个模型去推导出欧姆定律，我们发现电流与外加电场成正比，并且电导和材料内的自由电子密度N与弛豫时间有关
然而比热实验以及电导的温度相关无法用这一模型去解释，揭露了这一模型的失败之处，也就是说需要对这一模型进行进一步的修正
对模型进行修正首先要从它的假设入手，看有哪些不合理的地方
Drude把自由电子等价于理想气体，而学过统计物理我们知道，麦克斯韦玻尔兹曼统计有效
模型可以看出，越重的质量、越高的温度或越稀薄的密度更容易服从麦克斯韦玻尔兹曼统计
实际上就连氢气理想气体都能满足这个条件，所以我们可以说所有理想气体都可以用麦克斯韦玻尔兹曼统计
对于电子而言，由于其质量小、密度高，此条件变无法满足，所以麦克斯韦玻尔兹曼统计便无法应用
由于电子属于费米子，所以应当采用费米狄拉克分布
由于Drude当时处于量子观念肇始时期，只能说受到了时代的局限性
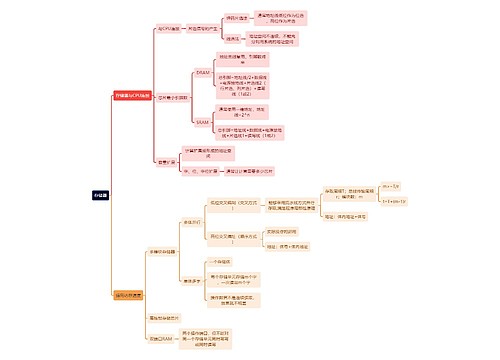
量子力学修正的自由电子模型(QMFEM)
1928年，索末菲将量子效应与费米狄拉克分布引入原有的drude模型
假设
电子气能量量子化，自由电子在导体中采用三微无限深势阱模型
电子服从泡利不相容原理
电子服从费米狄拉克分布
电子在0K会占据能级具有能量而不是像经典描述那样能量为0
沪公网安备 31011502019485号
上海工商