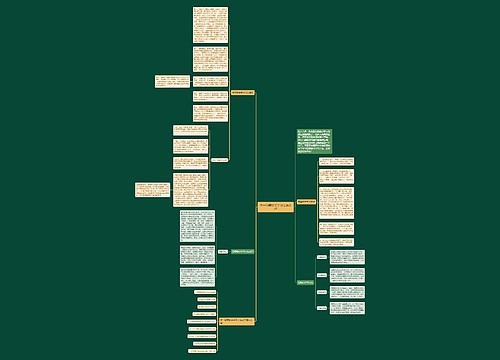
《高等数学》笔记思维导图
《高等数学》思维导图思维导图包含了重要的内容,其中第一讲包含了五种不同的极限类型和连续与间断相关内容,第二讲涵盖了微分方程的不同类型,如一阶、可分离和一阶齐次线性,和高阶线性微分方程的解题步骤,第三讲包含到常数项级数的性质和判断级数敛散的方法,包含审敛法、比较法和交错级数,同时还介绍了幂级数和傅里叶级数展开的相关概念和技巧,文中也提及了解题时可能会用到的极限性质、定义、保号性等。
思维导图大纲
《高等数学》笔记思维导图模板大纲
第一讲
极限
型一:夹逼定理以及n项和或积的极限
定积分应用
型二:单调有界数列必有极限
型三:变限积分函数的极限
型四:不定型
0/0,1^∞
∞/∞,0*∞,∞-∞,∞^0,0^0
型五:杂项
手法看情况
连续与间断
型一:间断点和分类
第二讲
微分方程
一阶
可分离(形式以及通解公式,下同)
齐次
一阶齐次线性
一阶非齐次线性
都不是
x<=>y ----> x=x(y)
可能会用到除上面的知识外:反函数求导
可降阶
缺y
缺x
高阶线性
预备
n阶齐次线性D.E.为(*),非齐次为(**),如果f(X)为两个函数只和,则有
若φ1(x),φ2(x).....φs(x)为(*)的解,那么有其线性组合也是(*)的解(充要条件)
若k1φ1(x)+k2φ2(x)+.....+ksφs(x)为(**)的解,那么有K1+...+Ks=1(充要条件)
二阶常系数齐次
背下解题步骤
三阶常系数齐次
解题步骤
二阶非齐次
型一:多项式乘指数函数
型二:含有三角函数
特解
是特征值:
不是特征值:
第三讲
常数项级数
性质
相加减
k倍
添加、改变、减少有限项,级数敛散性不变
添括号提高敛散性,反推不成立(用调和级数证)
级数收敛,通项在n趋于无穷时趋于0
两个参照
1/n的p次方
证调和级数发散(思想重要)
a乘q的n次方
正项级数
关于部分和
审敛法
比较法
基本形式:大收小也收,小散大也散
定理一(其实就是通项趋于0)
比值法(一般处理含阶乘)
定理二
根植法
定理三
积分法(一般出现ln)
定理四
交错级数
判别法—莱布尼兹法
和函数法(结合幂级数求和函数部分)
碰到给出一个常数项级数,直接问你等于多少
第一步:构造S(X),常数项级数为S(1/2)
第二部:利用幂级数知识求S(X)
绝对、条件收敛
本身收敛,加绝对值后发散
本身收敛,加绝对值后收敛
补充
收士收=收
发士发=?
收士发=发
一个级数敛散性与前有限项无关
添括号+收敛性
绝对值+发散性
解题往往会用到极限性质(定义、保号性等等)
平方会破坏交错,an收,an^ 2不一定收,若an大于等于0,就收
幂级数
定义
收敛半径、收敛域
性质
定理一:逐项可导性
定理二:逐项可积性
Notes
anX^n在X0处条件收敛
达朗贝审敛法
f(x)展开成级数
方法一:直接法
方法二:间接法—一般是化成有理函数
例子1
例子2
求和函数S(X)——公式1~7、2个逐项、微分方程
第一步求R,求两点
第二步选case
case1
case2,6、7靠不上就消灭分母
case3,123靠不上就微分方程
傅里叶级数
狄利克雷收敛性定理(背且字后面的公式)
周期为2L的函数的傅里叶展开(“~”:展开为,背下面)
[-L,L]上f(X)的展开
[-L,L]上f(X)是奇/偶的展开(f(x)为奇/偶函数)
奇->正弦,偶->余弦
[0,L]上f(X)展开正弦或者余弦
奇延拓-f(-x),以补充范围
偶延拓,f(-x),同样地
定积分中一个点的位置不影响结果
相关思维导图模板

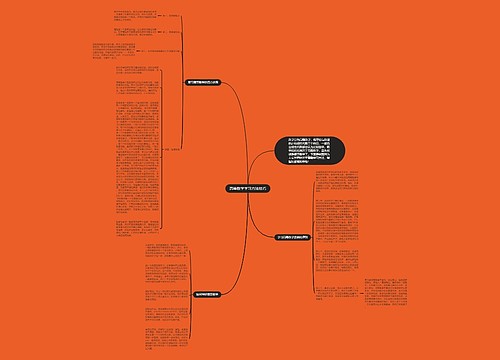
树图思维导图提供 大一高等数学学习方法技巧 在线思维导图免费制作,点击“编辑”按钮,可对 大一高等数学学习方法技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9229ef9480a93854153d9878a5ac1518

树图思维导图提供 高等数学学习方法技巧 在线思维导图免费制作,点击“编辑”按钮,可对 高等数学学习方法技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:fcac4876b300ed241aad32f384000c2d

















 上海工商
上海工商