高二数学必修3第三章要点解析:随机事件的概率思维导图
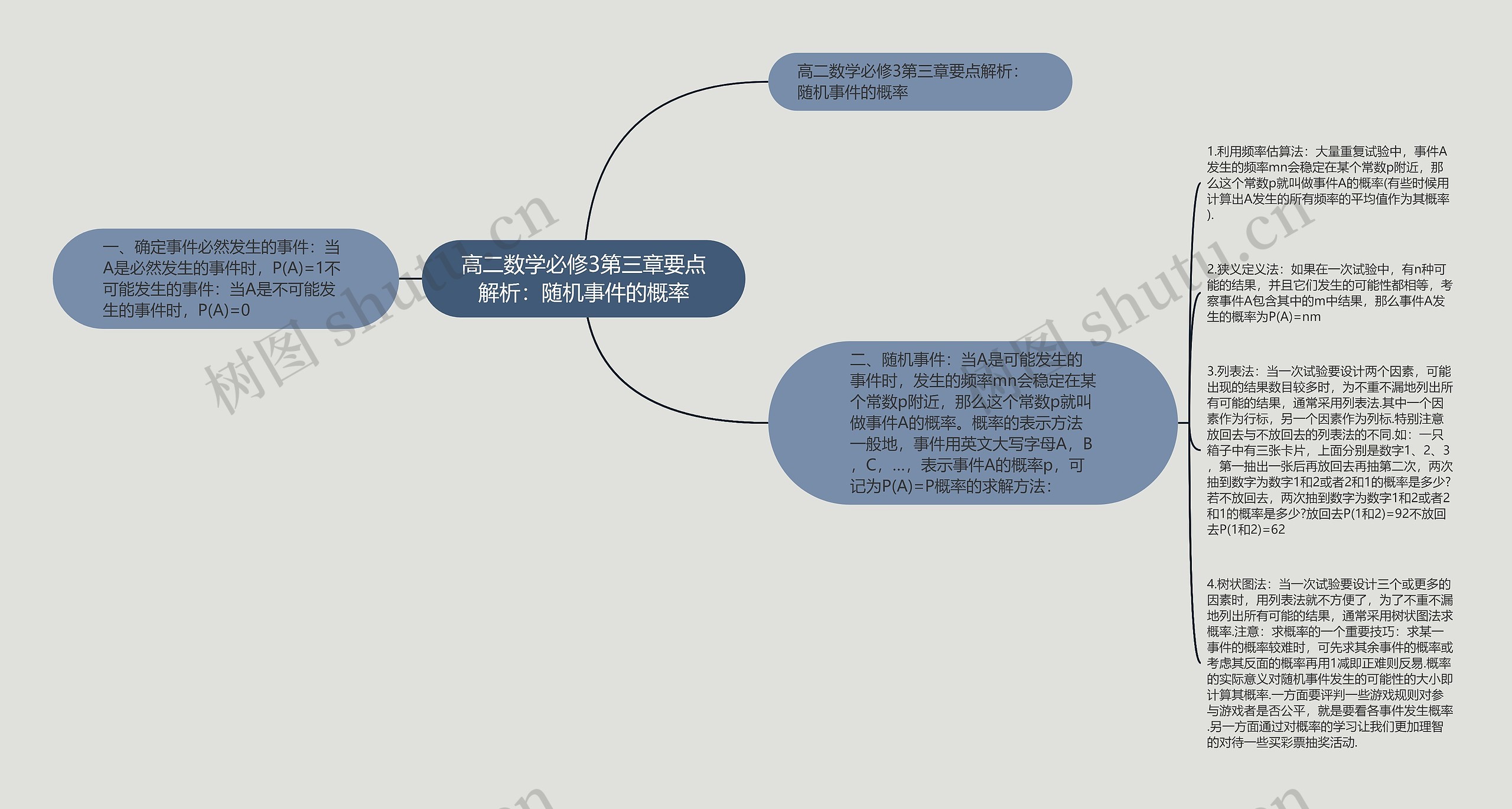
高二数学必修3第三章要点解析:随机事件的概率思维导图模板大纲,本章主要内容包含确定必然事件和不可能事件的概率,和随机事件的概率求解方法,对于必然发生的事件A,其概率P(A)等于1,对于不可能发生的事件A,其概率P(A)等于0。随机事件A是可能发生的事件,其发生频率会稳定在概率p附近,概率的表示方法一般用大写字母A、B、C,概率记为P(A),概率的求解方法有利用频率估算法、狭义定义法、列表法和树状图法。利用频率估算法是通过大量重复试验中事件A发生的频率来估计概率,狭义定义法是在一次试验中,有n种可能的结果且发生可能性相等时,事件A包含其中的m种结果的概率为P(A)=m/n,列表法适用于带有多个因素且结果数目较多的试验,需要列出所有可能的结果,并特别注意放回去与不放回去的情况,树状图法适用于设计三个或更多因素的试验,通过画树状图来列出所有可能的结果。对于求解概率较难的事件,可以先求其余事件的概率或考虑其反面的概率,再用1减去得到正面的概率,概率的实际意义在于评判游戏的公平性和对待彩票抽奖活动的理性。
思维导图大纲
高二数学必修3第三章要点解析:随机事件的概率思维导图模板大纲
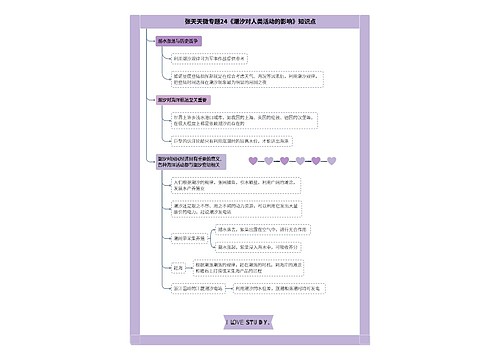
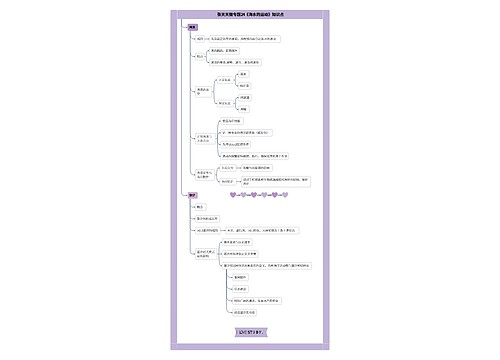
高二数学必修3第三章要点解析:随机事件的概率
一、确定事件必然发生的事件:当A是必然发生的事件时,P(A)=1不可能发生的事件:当A是不可能发生的事件时,P(A)=0
二、随机事件:当A是可能发生的事件时,发生的频率mn会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率。概率的表示方法一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P概率的求解方法:
1.利用频率估算法:大量重复试验中,事件A发生的频率mn会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率(有些时候用计算出A发生的所有频率的平均值作为其概率).
2.狭义定义法:如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,考察事件A包含其中的m中结果,那么事件A发生的概率为P(A)=nm
3.列表法:当一次试验要设计两个因素,可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.其中一个因素作为行标,另一个因素作为列标.特别注意放回去与不放回去的列表法的不同.如:一只箱子中有三张卡片,上面分别是数字1、2、3,第一抽出一张后再放回去再抽第二次,两次抽到数字为数字1和2或者2和1的概率是多少?若不放回去,两次抽到数字为数字1和2或者2和1的概率是多少?放回去P(1和2)=92不放回去P(1和2)=62
4.树状图法:当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.注意:求概率的一个重要技巧:求某一事件的概率较难时,可先求其余事件的概率或考虑其反面的概率再用1减即正难则反易.概率的实际意义对随机事件发生的可能性的大小即计算其概率.一方面要评判一些游戏规则对参与游戏者是否公平,就是要看各事件发生概率.另一方面通过对概率的学习让我们更加理智的对待一些买彩票抽奖活动.
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 9.战斗的基督教 在线思维导图免费制作,点击“编辑”按钮,可对 9.战斗的基督教 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:33d168acd0cd9f767f809c7a5df86e3a











 上海工商
上海工商