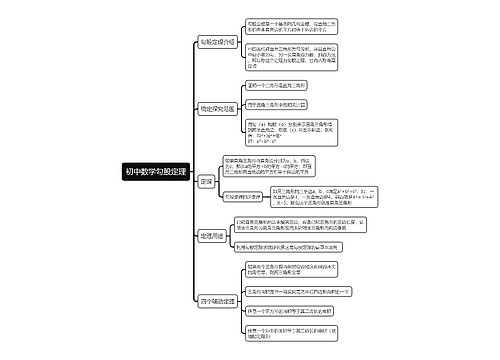
勾股定理思维导图
对勾股定理运用的探究和勾股定理逆命题的论证和应用，都是将图形与数量紧密的结合，以提高分析问题、解决问题的能力
树图思维导图提供 勾股定理思维导图 在线思维导图免费制作，点击“编辑”按钮，可对 勾股定理思维导图 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：d2e0eb9b7bdaeee3cc93faabbbd695b7
思维导图大纲
勾股定理思维导图模板大纲
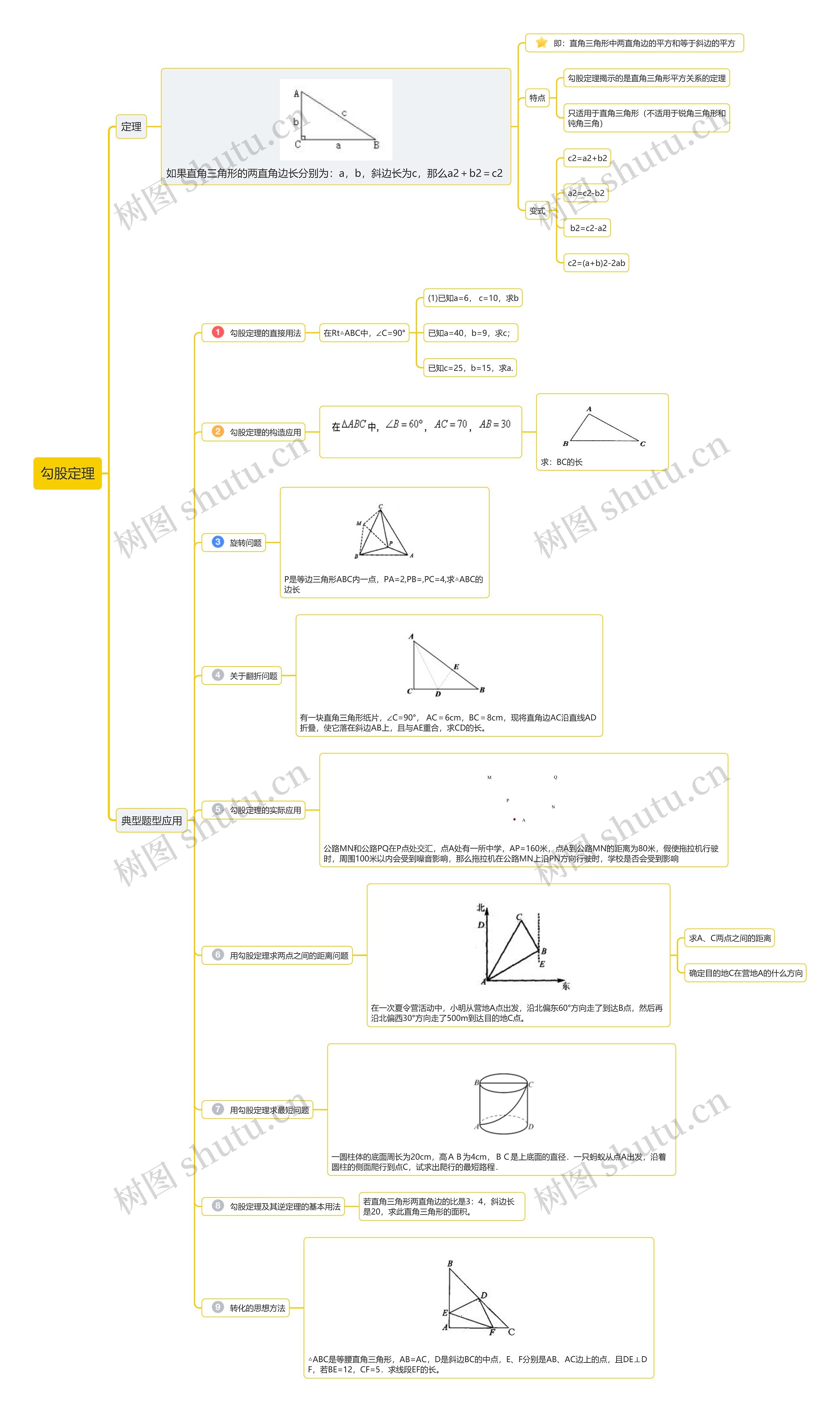
定理
如果直角三角形的两直角边长分别为：a，b，斜边长为c，那么a2＋b2＝c2
即：直角三角形中两直角边的平方和等于斜边的平方
特点
勾股定理揭示的是直角三角形平方关系的定理
只适用于直角三角形（不适用于锐角三角形和钝角三角）
变式
c2=a2+b2
a2=c2-b2
b2=c2-a2
c2=(a+b)2-2ab
典型题型应用
勾股定理的直接用法
在Rt△ABC中，∠C=90°
(1)已知a=6， c=10，求b
已知a=40，b=9，求c；
已知c=25，b=15，求a.
勾股定理的构造应用
求：BC的长
旋转问题
P是等边三角形ABC内一点，PA=2,PB=,PC=4,求△ABC的边长
关于翻折问题
有一块直角三角形纸片，∠C=90°， AC＝6cm，BC＝8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长。
勾股定理的实际应用
公路MN和公路PQ在P点处交汇，点A处有一所中学，AP=160米，点A到公路MN的距离为80米，假使拖拉机行驶时，周围100米以内会受到噪音影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到影响
用勾股定理求两点之间的距离问题
在一次夏令营活动中，小明从营地A点出发，沿北偏东60°方向走了到达B点，然后再沿北偏西30°方向走了500m到达目的地C点。
求A、C两点之间的距离
确定目的地C在营地A的什么方向
用勾股定理求最短问题
一圆柱体的底面周长为20cm，高ＡＢ为4cm，ＢＣ是上底面的直径．一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，试求出爬行的最短路程．
勾股定理及其逆定理的基本用法
若直角三角形两直角边的比是3：4，斜边长是20，求此直角三角形的面积。
转化的思想方法
△ABC是等腰直角三角形，AB=AC，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF，若BE=12，CF=5．求线段EF的长。
沪公网安备 31011502019485号
上海工商