一次函数人教版数学八年级上册教案思维导图

笔灵AI论文写作三步搞定，GO>>

当前位置:树图

思维导图模板

基础教育

数学

一次函数人教版数学八年级上册教案思维导图

免费下载

免费使用文件

好想你

浏览量：3

2023-04-04 22:20:58

已被使用0次

查看详情

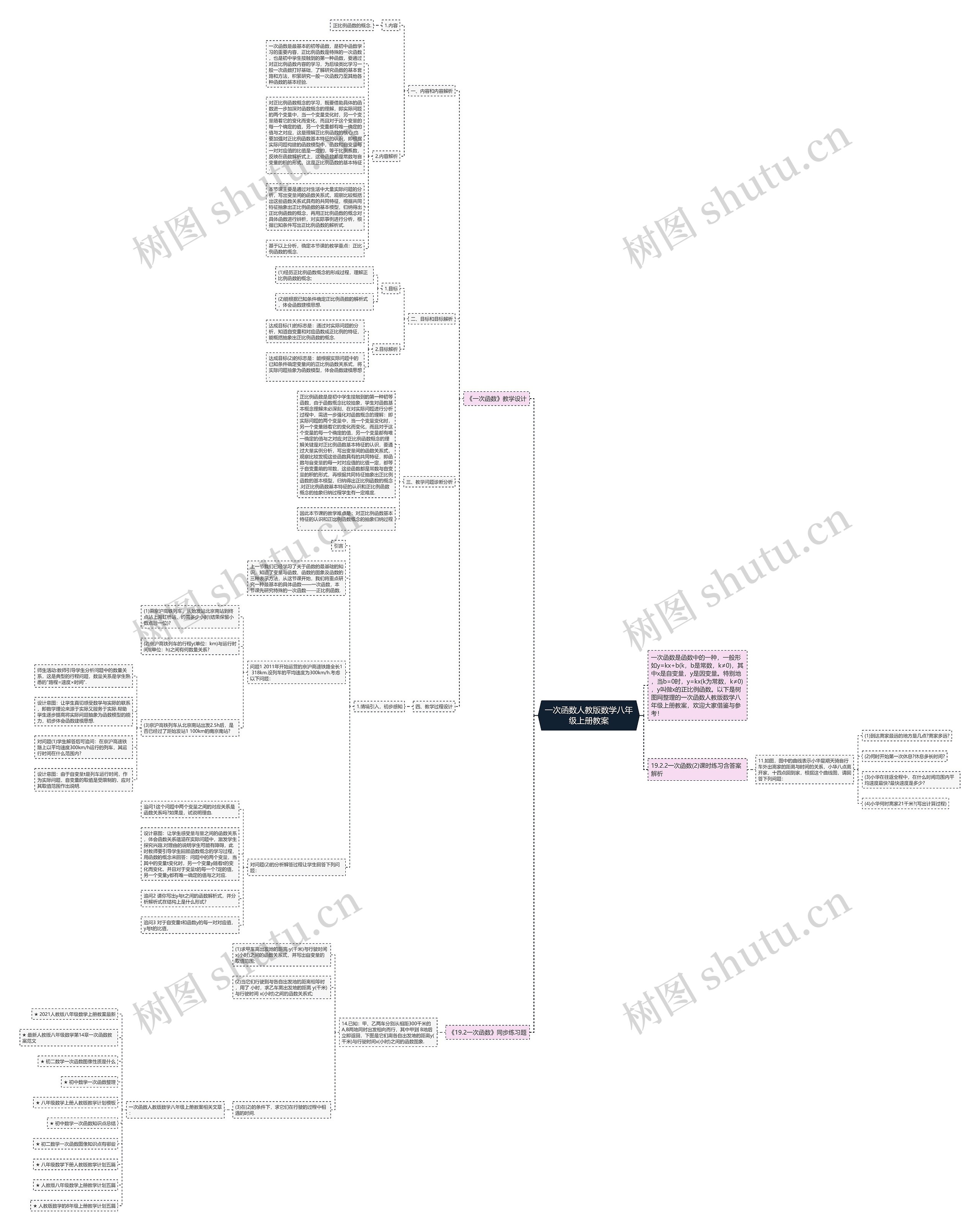
一次函数人教版数学八年级上册教案思维导图中，重要的知识点有一次函数的定义和特点，和正比例函数的概念和基本特征，一次函数通常形式为y=kx+b(k和b为常数)，其中x为自变量，y为因变量，而正比例函数是一次函数中一种特殊的形式，当b=0时，y=kx(k为常数，k≠0)，这时y是x的正比例函数。学习正比例函数对后续学习其他函数打好基础，要通过实际问题的分析来理解正比例函数的核心，即实际问题的两个变量中，当一个变量变化时，另一个变量随之变化，对于每个确定的值，另一个变量都有唯一的值与之对应。学习正比例函数的基本特征，即函数和自变量每一对对应值的比值是一定的，等于比例系数，本课程设计通过实例分析，让学生更好的理解正比例函数的概念与基本特征，并能根据实际问题确定正比例函数的解析式，从中体会函数建模思想。

一次函数数学八年级教案一次函数数学八年级教案

举报/反馈

思维导图大纲

一次函数人教版数学八年级上册教案思维导图模板大纲

一次函数是函数中的一种，一般形如y=kx+b(k，b是常数，k≠0)，其中x是自变量，y是因变量。特别地，当b=0时，y=kx(k为常数，k≠0)，y叫做x的正比例函数。以下是树图网整理的一次函数人教版数学八年级上册教案，欢迎大家借鉴与参考！

《一次函数》教学设计

一、内容和内容解析

1.内容

正比例函数的概念.

2.内容解析

一次函数是最基本的初等函数，是初中函数学习的重要内容，正比例函数是特殊的一次函数，也是初中学生接触到的第一种函数，要通过对正比例函数内容的学习，为后续类比学习一般一次函数打好基础，了解研究函数的基本套路和方法，积累研究一般一次函数乃至其他各种函数的基本经验.

对正比例函数概念的学习，既要借助具体的函数进一步加深对函数概念的理解，即实际问题的两个变量中，当一个变量变化时，另一个变量随着它的变化而变化，而且对于这个变量的每一个确定的值，另一个变量都有唯一确定的值与之对应，这是理解正比例函数的核心;也要加强对正比例函数基本特征的认识，即根据实际问题构建的函数模型中，函数和自变量每一对对应值的比值是一定的，等于比例系数，反映在函数解析式上，这些函数都是常数与自变量的积的形式，这是正比例函数的基本特征.

本节课主要是通过对生活中大量实际问题的分析，写出变量间的函数关系式，观察比较概括出这些函数关系式具有的共同特征，根据共同特征抽象出正比例函数的基本模型，归纳得出正比例函数的概念，再用正比例函数的概念对具体函数进行辨析，对实际事例进行分析，根据已知条件写出正比例函数的解析式.

基于以上分析，确定本节课的教学重点：正比例函数的概念.

二、目标和目标解析

1.目标

(1)经历正比例函数概念的形成过程，理解正比例函数的概念;

(2)能根据已知条件确定正比例函数的解析式，体会函数建模思想.

2.目标解析

达成目标(1)的标志是：通过对实际问题的分析，知道自变量和对应函数成正比例的特征，能概括抽象出正比例函数的概念.

达成目标(2)的标志是：能根据实际问题中的已知条件确定变量间的正比例函数关系式，将实际问题抽象为函数模型，体会函数建模思想.

三、教学问题诊断分析

正比例函数是是初中学生接触到的第一种初等函数，由于函数概念比较抽象，学生对函数基本概念理解未必深刻，在对实际问题进行分析过程中，需进一步强化对函数概念的理解：即实际问题的两个变量中，当一个变量变化时，另一个变量随着它的变化而变化，而且对于这个变量的每一个确定的值，另一个变量都有唯一确定的值与之对应;对正比例函数概念的理解关键是对正比例函数基本特征的认识，要通过大量实例分析，写出变量间的函数关系式，观察比较发现这些函数具有的共同特征，即函数与自变量的每一对对应值的比值一定，都等于自变量前的常数，这些函数都是常数与自变量的积的形式，再根据共同特征抽象出正比例函数的基本模型，归纳得出正比例函数的概念.对正比例函数基本特征的认识和正比例函数概念的抽象归纳过程学生有一定难度.

因此本节课的教学难点是：对正比例函数基本特征的认识和正比例函数概念的抽象归纳过程.

四、教学过程设计

1.情境引入，初步感知

引言

上一节我们已经学习了关于函数的最基础的知识，知道了变量与函数、函数的图象及函数的三种表示方法，从这节课开始，我们将重点研究一种最基本的具体函数——一次函数，本节课先研究特殊的一次函数——正比例函数.

问题1 2011年开始运营的京沪高速铁路全长1 318km.设列车的平均速度为300km/h.考虑以下问题：

(1)乘京沪高铁列车，从始发站北京南站到终点站上海虹桥站，约需多少小时(结果保留小数点后一位)?

(2)京沪高铁列车的行程y(单位：km)与运行时间t(单位：h)之间有何数量关系?

(3)京沪高铁列车从北京南站出发2.5h后，是否已经过了距始发站1 100km的南京南站?

师生活动:教师引导学生分析问题中的数量关系，这是典型的行程问题，数量关系是学生熟悉的"路程=速度×时间".

设计意图：让学生真切感受数学与实际的联系，即数学理论来源于实际又服务于实际.帮助学生逐步提高将实际问题抽象为函数模型的能力，初步体会函数建模思想.

对问题(1)学生解答后可追问：在京沪高速铁路上以平均速度300km/h运行的列车，其运行时间在什么范围内?

设计意图：由于自变量t是列车运行时间，作为实际问题，自变量的取值是受限制的，应对其取值范围作出说明.

对问题(2)的分析解答过程让学生回答下列问题：

追问1这个问题中两个变量之间的对应关系是函数关系吗?如果是，试说明理由.

设计意图：让学生感受量与量之间的函数关系，体会函数关系蕴涵在实际问题中，激发学生探究兴趣.对理由的说明学生可能有障碍，此时教师要引导学生回顾函数概念的学习过程，用函数的概念来回答：问题中的两个变量，当其中的变量t变化时，另一个变量y随着t的变化而变化，并且对于变量t的每一个?定的值，另一个变量y都有唯一确定的值与之对应.

追问2 请你写出y与t之间的函数解析式，并分析解析式在结构上是什么形式?

追问3 对于自变量t和函数y的每一对对应值，y与t的比值，