人教版2018七年级数学上册期末试题附答案解释(一元一次方程)思维导图
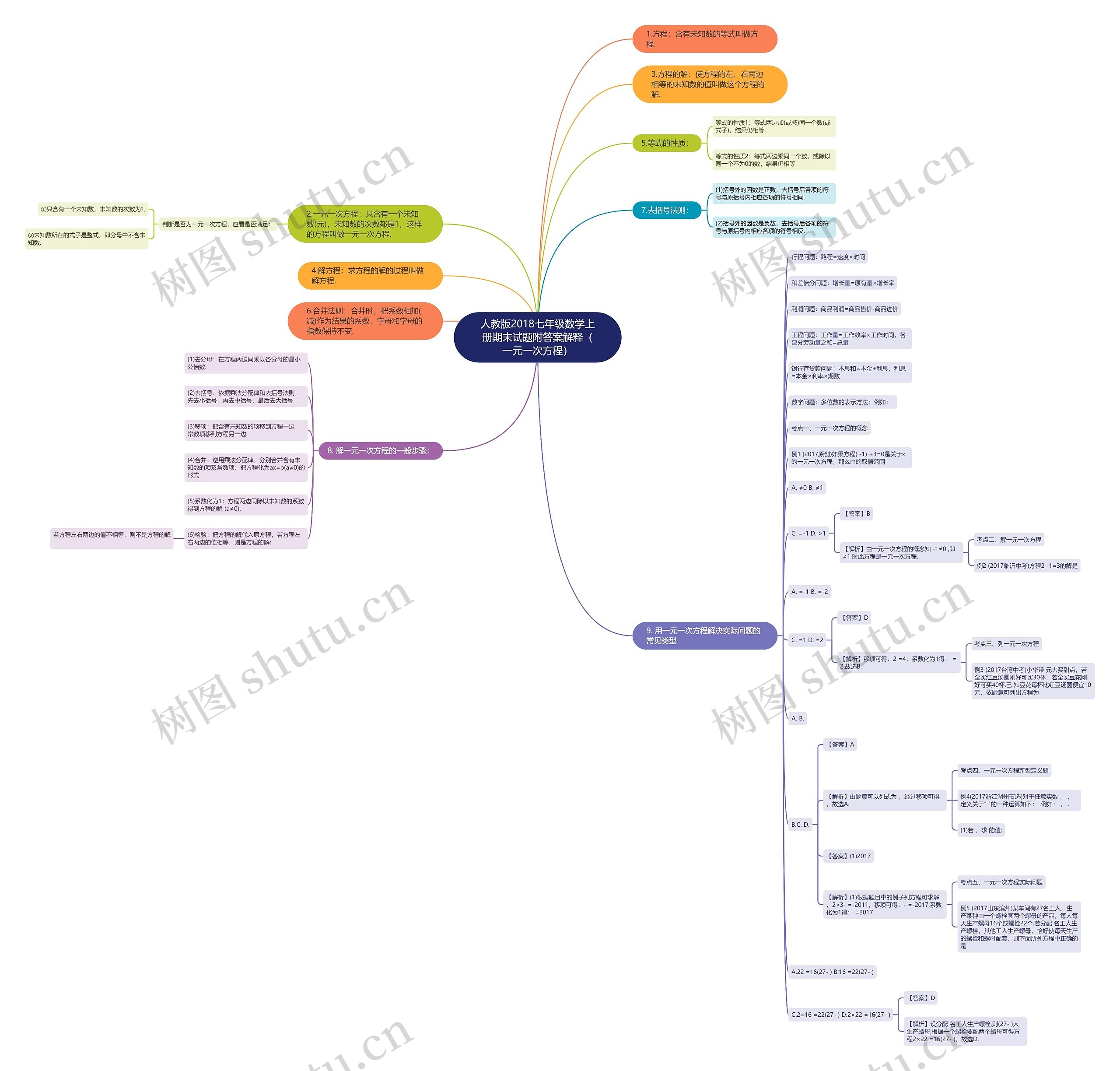
模板展示了人教版2018七年级数学上册期末试题中与一元一次方程相关的内容,包含一元一次方程的概念、判断、解法、列方程法和用一元一次方程解决实际问题的常见类型。一元一次方程具体的判断方法和解法步骤都有详细的介绍,一些具体的例题,帮助读者理解和掌握知识点,包含解一元一次方程、列一元一次方程和一元一次方程实际问题。
思维导图大纲
人教版2018七年级数学上册期末试题附答案解释(一元一次方程)思维导图模板大纲
1.方程:含有未知数的等式叫做方程.
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.
判断是否为一元一次方程,应看是否满足:
①只含有一个未知数,未知数的次数为1;
②未知数所在的式子是整式,即分母中不含未知数.
3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.
4.解方程:求方程的解的过程叫做解方程.
5.等式的性质:
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
6.合并法则:合并时,把系数相加(减)作为结果的系数,字母和字母的指数保持不变.
7.去括号法则:
(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.
8. 解一元一次方程的一般步骤:
(1)去分母:在方程两边同乘以各分母的最小公倍数.
(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.
(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.
(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax=b(a≠0)的形式.
(5)系数化为1:方程两边同除以未知数的系数得到方程的解 (a≠0).
(6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;
若方程左右两边的值不相等,则不是方程的解.
9. 用一元一次方程解决实际问题的常见类型
行程问题:路程=速度×时间
和差倍分问题:增长量=原有量×增长率
利润问题:商品利润=商品售价-商品进价
工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量
银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数
数字问题:多位数的表示方法:例如: .
考点一、一元一次方程的概念
例1 (2017原创)如果方程( -1) +3=0是关于x的一元一次方程,那么m的取值范围
A. ≠0 B. ≠1
C. =-1 D. >1
【答案】B
【解析】由一元一次方程的概念知 -1≠0 ,即 ≠1 时此方程是一元一次方程.
考点二、解一元一次方程
例2 (2017临沂中考)方程2 -1=3的解是
A. =-1 B. =-2
C. =1 D. =2
【答案】D
【解析】移项可得:2 =4,系数化为1得: =2.故选B.
考点三、列一元一次方程
例3 (2017台湾中考)小华带 元去买甜点,若全买红豆汤圆刚好可买30杯,若全买豆花刚好可买40杯.已 知豆花每杯比红豆汤圆便宜10元,依题意可列出方程为
A. B.
B.C. D.
【答案】A
【解析】由题意可以列式为 ,经过移项可得 ,故选A.
考点四、一元一次方程新型定义题
例4(2017浙江湖州节选)对于任意实数 , ,定义关于" "的一种运算如下: .例如: , .
(1)若 ,求 的值;
【答案】(1)2017
【解析】(1)根据题目中的例子列方程可求解,2×3- =-2011,移项可得:- =-2017;系数化为1得: =2017.
考点五、一元一次方程实际问题
例5 (2017山东滨州)某车间有27名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺母16个或螺栓22个.若分配 名工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下面所列方程中正确的是
A.22 =16(27- ) B.16 =22(27- )
C.2×16 =22(27- ) D.2×22 =16(27- )
【答案】D
【解析】设分配 名工人生产螺栓,则(27- )人生产螺母,根据一个螺栓要配两个螺母可得方程2×22 =16(27- ),故选D.


















 上海工商
上海工商