2015高考数学指数函数与对数函数公式汇总思维导图
会员免费下载或30积分
会员免费使用或30积分
晚间拾梦 浏览量:32023-04-20 18:38:57
已被使用1次
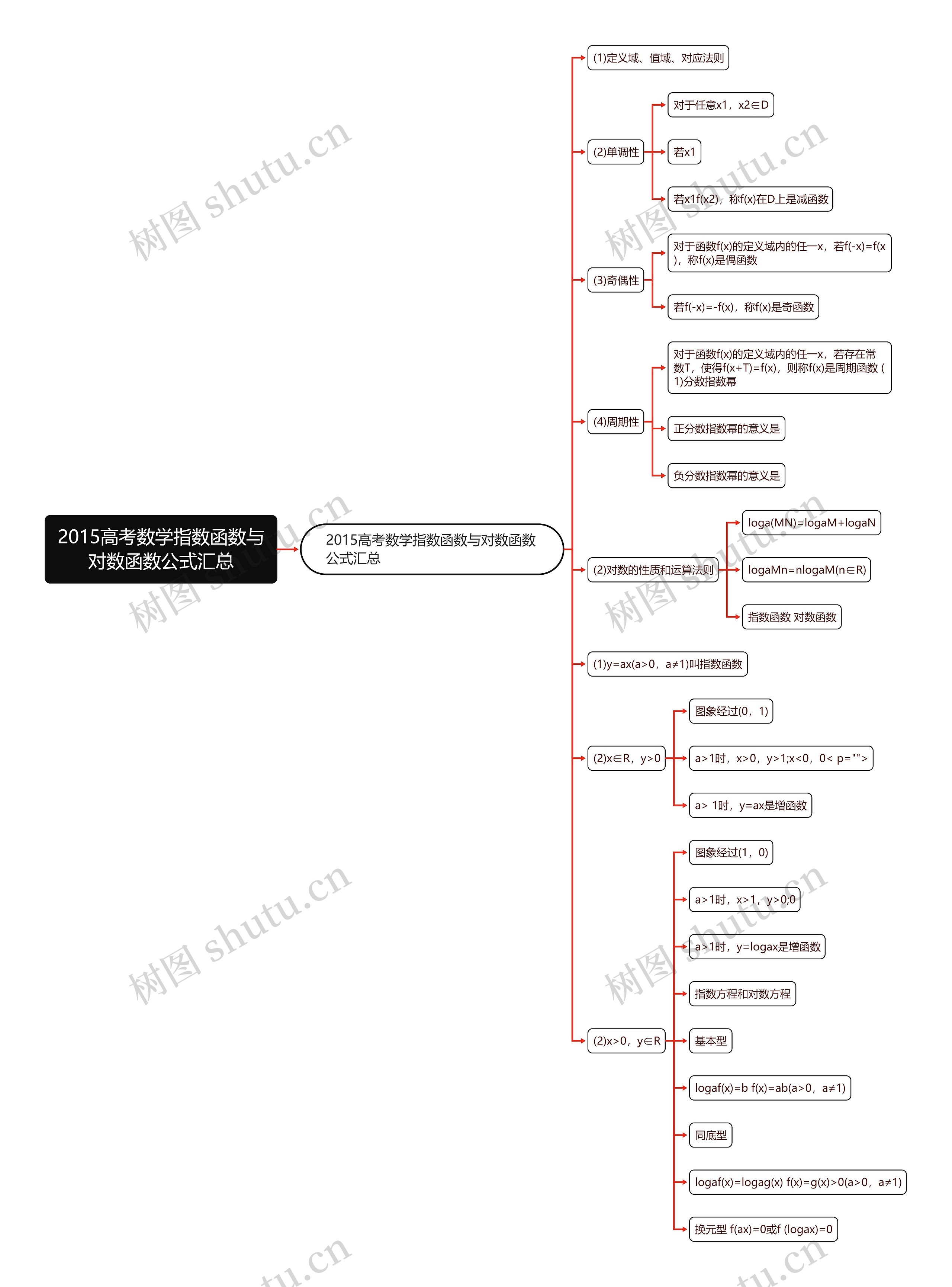
2015高考数学指数函数与对数函数公式汇总思维导图是一个汇总了知识点的模板大纲,包含了指数函数和对数函数的定义域、值域、对应法则、单调性、奇偶性和周期性,另外还包含了分数指数幂的意义和对数的性质与运算法则,指数函数的图象经过(0,1),当a大于1时是增函数。对数函数的图象经过(1,0),当a大于1时是增函数,还介绍了指数方程和对数方程的基本型、同底型和换元型,这些知识点是2015高考数学中指数函数与对数函数的重要考点。
思维导图大纲
2015高考数学指数函数与对数函数公式汇总思维导图模板大纲
2015高考数学指数函数与对数函数公式汇总
(1)定义域、值域、对应法则
(2)单调性
对于任意x1,x2∈D
若x1
若x1f(x2),称f(x)在D上是减函数
(3)奇偶性
对于函数f(x)的定义域内的任一x,若f(-x)=f(x),称f(x)是偶函数
若f(-x)=-f(x),称f(x)是奇函数
(4)周期性
对于函数f(x)的定义域内的任一x,若存在常数T,使得f(x+T)=f(x),则称f(x)是周期函数 (1)分数指数幂
正分数指数幂的意义是
负分数指数幂的意义是
(2)对数的性质和运算法则
loga(MN)=logaM+logaN
logaMn=nlogaM(n∈R)
指数函数 对数函数
(1)y=ax(a>0,a≠1)叫指数函数
(2)x∈R,y>0
图象经过(0,1)
a>1时,x>0,y>1;x<0,0< p="">
a> 1时,y=ax是增函数
(2)x>0,y∈R
图象经过(1,0)
a>1时,x>1,y>0;0
a>1时,y=logax是增函数
指数方程和对数方程
基本型
logaf(x)=b f(x)=ab(a>0,a≠1)
同底型
logaf(x)=logag(x) f(x)=g(x)>0(a>0,a≠1)
换元型 f(ax)=0或f (logax)=0










 上海工商
上海工商