考研数学常考题型(线性代数篇)思维导图
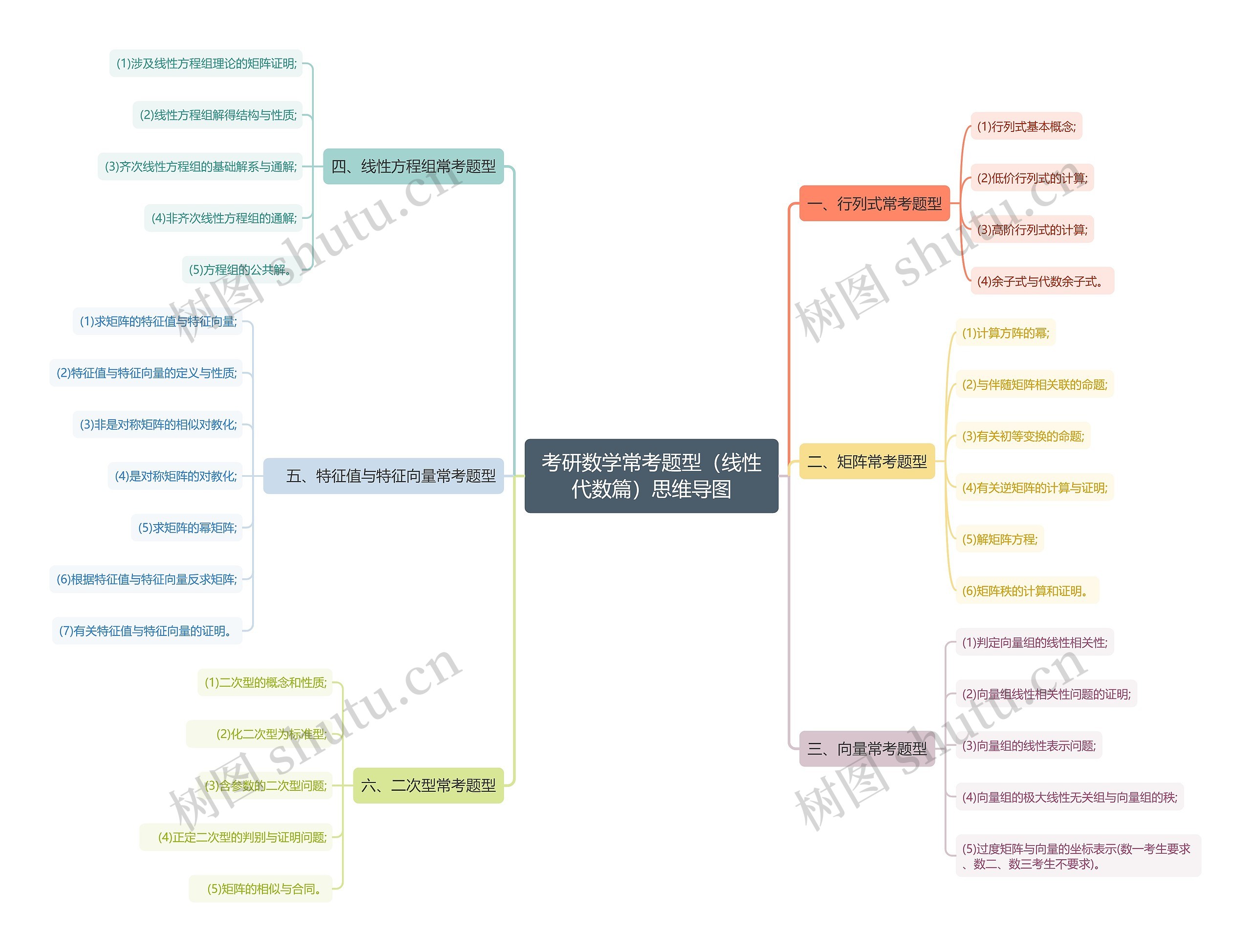
考研数学常考题型(线性代数篇)思维导图,包含行列式、矩阵、线性方程组、向量、特征值与特征向量、二次型等内容,行列式常考题型概括了基本概念、低价行列式与高阶行列式的计算和余子式与代数余子式,矩阵常考题型包含计算方阵的幂、伴随矩阵的相关性、初等变换的命题、逆矩阵的计算与证明、矩阵方程的解、矩阵秩的计算与证明,线性方程组常考题型则关注于包含线性方程组理论的矩阵证明、线性方程组解得结构与性质、齐次线性方程组的基础解系与通解、非齐次线性方程组的通解和方程组的公共解,向量常考题型涵盖了判定向量组的线性相关性、向量组线性相关性问题的证明、向量组的线性表示问题、向量组的极大线性无关组与向量组的秩、过度矩阵与向量的坐标表示,特征值与特征向量常考题型则聚焦于求矩阵的特征值与特征向量、特征值与特征向量的定义与性质、非对称矩阵的相似对角化、对称矩阵的对角化、求矩阵的幂矩阵、根据特征值与特征向量反求矩阵和有关特征值与特征向量的证明,二次型常考题型则包含二次型的概念和性质、化二次型为标准型、含参数的二次型问题、正定二次型的判别与证明问题和矩阵的相似与合同。
思维导图大纲
考研数学常考题型(线性代数篇)思维导图思维导图模板大纲
一、行列式常考题型
(1)行列式基本概念;
(2)低价行列式的计算;
(3)高阶行列式的计算;
(4)余子式与代数余子式。
二、矩阵常考题型
(1)计算方阵的幂;
(2)与伴随矩阵相关联的命题;
(3)有关初等变换的命题;
(4)有关逆矩阵的计算与证明;
(5)解矩阵方程;
(6)矩阵秩的计算和证明。
四、线性方程组常考题型
(1)涉及线性方程组理论的矩阵证明;
(2)线性方程组解得结构与性质;
(3)齐次线性方程组的基础解系与通解;
(4)非齐次线性方程组的通解;
(5)方程组的公共解。
三、向量常考题型
(1)判定向量组的线性相关性;
(2)向量组线性相关性问题的证明;
(3)向量组的线性表示问题;
(4)向量组的极大线性无关组与向量组的秩;
(5)过度矩阵与向量的坐标表示(数一考生要求、数二、数三考生不要求)。
五、特征值与特征向量常考题型
(1)求矩阵的特征值与特征向量;
(2)特征值与特征向量的定义与性质;
(3)非是对称矩阵的相似对教化;
(4)是对称矩阵的对教化;
(5)求矩阵的幂矩阵;
(6)根据特征值与特征向量反求矩阵;
(7)有关特征值与特征向量的证明。
六、二次型常考题型
(1)二次型的概念和性质;
(2)化二次型为标准型;
(3)含参数的二次型问题;
(4)正定二次型的判别与证明问题;
(5)矩阵的相似与合同。



















 上海工商
上海工商