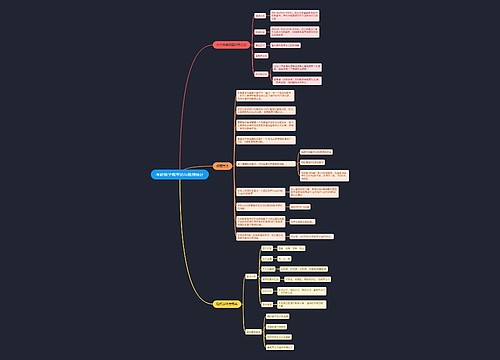
《统计描述》思维导图
简述《统计学》中计数资料的统计描述
树图思维导图提供 《统计描述》 在线思维导图免费制作，点击“编辑”按钮，可对 《统计描述》 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：3443a755d31b182518cef4e4dbe62a73
思维导图大纲
《统计描述》思维导图模板大纲
多个样本均数比较的方差分析
适用条件
计量资料、方差齐、独立性、正态性
用于两组或两组以上的总体均数的比较
基本思想
变异分解：
设处理因素有g（g≥2）个不同的水平，实验对象（对人称为受试对象）随机分为g组，分别接受不同水平的干预。
方差分析的目的就是在Ho：μ1=μ2…=μg成立的条件下，通过分析各处理组均数之间的差别大小，推断g个总体均数间有无差别，从而说明处理因素的效果是否存在。
总变异
所有个体值与总均数之间的差异
用离均差平方和（SS）表示，即各观测值Xij与总均数X-差值的平方和，记为SS总，计算公式为
组间变异
不同组别之间的差异。除随机误差外，还与各组施加的处理因素有关。
用各组均数Xi-与总均数X-的离均差平方和表示，记为SS组间，计算公式为
组内变异
同一组别内部，各观察值与该组均数的差异。主要由组内观察对象的个体差异和随机测量误差造成的，统称为随机误差。
组内变异用各观测值Xij与其所在组的均数Xi-的差值的平方和表示，计算公式为
各离均差平方和的自由度为
总离均差平方和分解为组间离均差平方和与组内离均差平方和
总自由度分解为组间自由度和组内自由度
均方
各部分离均差平方和不能直接比较，需将各部分离均差平方和除以相应自由度，其比值称为均方差（MS）
F 统计量
组间均方与组内均方的比值
基本步骤
建立假设检验，确定检验水准
H0：μ1=μ2=μ3，即三组总体均数相等
H1：μi不全相等，即三组总体均数不全相等
α=0.05
计算检验统计量
确定P值，得出结论
完全随机设计资料的方差分析
完全随机设计
随机：机会均等的原则。每个受试者都有机会进入试验组或对照组。
随机≠随意
随机的目的：避免选择偏倚、混杂偏倚
可以使已知的或潜在的影响因素在处理组间保持均衡。
试验研究中，将n个研究对象随机分配到k个处理组中，分别接受不同的处理，观察实验效应。
均衡设计：各组样本量相等。此时，统计检验效率最高。
方差分析
随机区组设计资料的方差分析
又称配伍组设计，先将受试对象按条件相同或相近组成m个区组，每个区组中有k个受试对象，再随机将k个受试对象分到k个处理组中。
两因素：处理因素和区组因素
注意
当方差分析组间效应有统计学意义时，表示至少有两组的总体均数不同，需要采用多重比较进一步分析组与组之间的差别。
即方差分析进行的是整体的比较，当整体有意义时，需要进行两两比较来分析哪两组间有差异。
多个样本均数间的多重比较
是在方差分析有统计学意义的基础上进行的深入分析，探索多组均数中，哪两组间差别，哪两组间没有差别。又称为方差分析的后续检验（post hoc test）。
两两比较时，要采用特定的两两比较方法，而不能直接采用t检验进行多次的两组间比较，会增大I型错误的概率。
常用的方法有LSD-t和SNK检验。
计数资料的统计描述
绝对数：实际观察所得
相对数：率、构成比、相对比
率（强度相对数）
构成比（结构相对数）
比（相对比）
应用相对数的注意事项
结构相对数（构成比）不能代替强度相对数（率）。构成比是用以说明事物内部某种构成所占比重或分布，并不说明某现象发生的频率或强度。
计算相对数应有足够数量。例数较少会使相对数波动较大。
正确计算合计率（平均率）。不能简单由各组率相加或平均而得，要用合计的有关实际数字计算。
注意资料的可比性。比较相对数时，除了要对比的因素，其余的影响因素应尽可能相同或相近。随机抽样原则进行分组。
相关思维导图模板
树图思维导图提供 统计 在线思维导图免费制作，点击“编辑”按钮，可对 统计 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：d814adf3d5c49be52df99af7591514a6
树图思维导图提供 人教版小学4年级数学下册考试重点 在线思维导图免费制作，点击“编辑”按钮，可对 人教版小学4年级数学下册考试重点 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：4703d6c90764abec6fa1650d98d37a0e
沪公网安备 31011502019485号
上海工商